View this report in PDF here.
How does computational thinking affect students’ understanding and
experiences in tertiary mathematics?
By Erin Clements, McMaster University, October 2018
I have been teaching the undergraduate course Calculus for Life Sciences (Math 1LS3) for approximately 10 years at McMaster University. Each semester I watch students struggle with applying mathematics in context, that is, connecting the abstract concepts taught in a traditional mathematics course to the practical mathematics found in journal articles.
Through my work as a research assistant for Dr. George Gadanidis, I was introduced to several math and coding initiatives being implemented by the Wellington District Catholic School Board. What I found most intriguing was a dual credit course, which integrated mathematics and computer science, thus covering two streams of material at once. This integrated approach was appealing to me for a number of reasons and it inspired me to research a similar approach at the tertiary level.

Why integrate coding into an applied calculus course?
Incorporating coding activities into Math 1LS3 provides an alternative way to explore the mathematical concepts traditionally taught in a first-year calculus course. This has the potential to increase the engagement of students (and instructors!), while better accommodating a diverse group of students with varying learning styles and abilities. As well, exploring mathematical models and algorithms using code offers a more dynamic experience for students, which traditional paper and pencil activities cannot provide. For example, students are able to make predictions, reason intuitively about relationships, and easily interact with the variables and parameters and receive immediate feedback. Moreover, integrating technology into our mathematical explorations allows us to keep the applications meaningful and authentic (for instance, we are not forced to oversimplify examples to make them more manageable to compute), and better aligns our activities with current practices in the field. By integrating this component into a preexisting mathematics course, students have an opportunity to enrich their mathematical understanding and develop a working knowledge of a modern computer language (a valuable skill in an increasingly computational world!), without taking an additional course explicitly in computer programming.
An example:
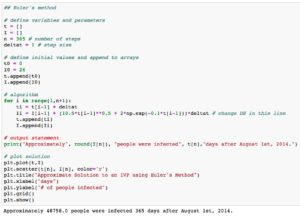
Euler’s method is an algorithm used to approximate solutions of first-order differential equations, given initial conditions. In Math 1LS3, students are asked to approximate the solution to a single differential equation by applying Euler’s method for a maximum of four steps, thus obtaining a superficial, uninteresting, yet easy to compute, result.
By exploring the initial value problem with code, students are able to investigate the behaviour of the model over a longer period (say, over months or even years) as well as increase the accuracy of their estimations (by decreasing the step size), an activity that would be unwieldy without computer technology.
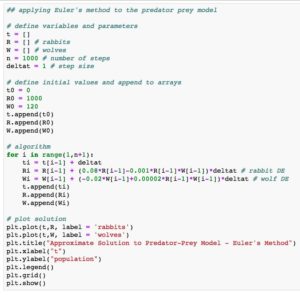
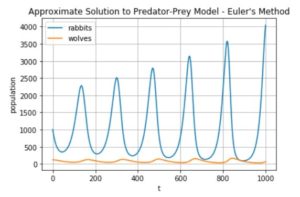
Moreover, using code, this algorithm can easily be extended to systems of first-order differential equations where students can explore more complex models, such as the SEIR-model, used to study the spread of the EBOLA virus during the recent epidemic or the classic predator-prey model, which investigates the dynamics between two species interacting in a common habitat.
The project:
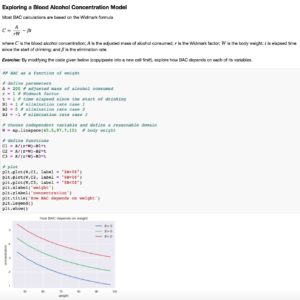
Together with my colleague Miroslav Lovric, I created a series of coding activities to complement the mathematical material studied in Math 1LS3, which has an enrollment of approximately 1000 students in the fall of 2018 semester. These activities are organized into four labs, which correspond to the main themes in the course: mathematical models, limits and derivatives, differential equations and integrals, and discrete-time dynamical systems. Students download these labs from the course webpage (https://ms.mcmaster.ca/lovric/1LS3.html) and work on them in Jupyter Notebook, a free online platform, which supports Python code. Being mindful that the course is primarily a mathematics course, we present the coding as a numerical approach to the mathematical ideas and focus on directly applying the code, rather than teaching nuances of the Python language. Brief explanations are provided as needed in the form of comments throughout the code (for example, x = np.linspace(1, 4, 10) # creates an array of 10 equally spaced x-values between 1 and 4). Students are encouraged to explore models, algorithms, etc. by copying, pasting, and modifying the code in each cell.
Sample activity (modified) from Lab 1 in Math 1LS3:
At the end of each lab, students are asked to respond to a series of narrative questions, which invite students to reflect on their learning experiences throughout the lab.
Sample survey questions from Lab 2:
Quotations taken from narrative responses on Lab 1:
“I think it [coding] is a great addition to Math 1LS3 because scientists often have to work with lots of data and it helps to understand how the data analysis of a software works rather than simply using it.”
“One aspect that was effective was how intuitive some of the questions were because they gave the possibility to experiment with the given functions and their graphs to discover their behavior without the hassle of having to redraw the graphs by hand.”
“It seamlessly integrated math and computer science into one task. Not only did it aid in deepening my math knowledge, but also enabled me to understand math through coding. The module was also not too long and very clear, allowing me to really enjoy the task at hand.”
I look forward to analyzing the data at the end of the semester and contributing my research to the ongoing project, Computational Thinking in Mathematics Education.
For more information, please contact Erin Clements (clemene@math.mcmaster.ca).